这将是一个非常口语化的总结，因为这就是我口述的总结。

语法分析过程主要包括两种方法：自底向上的语法分析和自顶向下的语法分析。其中，“底”指的就是原始串，而“顶”指的是开始符号。分析的目的就是确定某一个确定的字符串是否属于文法描述的语言。

而这些分析方法，最终都是要让串形成对应的语法分析树，因此它们将一个判定问题，转化成了生成语法分析树的过程。

First集和Follow集

First集和Follow集应该是对于任意的文法都是能够确定的。

文法中的任意文法符号串都是有First集的，First集相当于这个文法符号串能推出的串中最左侧的终结符的集合。First集可以包含$\epsilon$。

求First集的规则：

  1. 把所有的终结符语法规则列出来（我感觉First集求的时候不能有或？还是也可以）

  2. 如果X是终结符或者$\epsilon$,$First(X)={X}$

    如果X是非终结符，对每个产生式$X->X_1X_2…X_n$,$First(X_1)$是$First(X)$的子集。

    如果有$X_1X_2…X_i\Rightarrow\epsilon(i<n)$,那么$First(X_{i+1})$是$First(X)$的子集。

Follow集能够让一个非终结符消失（推出空），就是说Follow是确定当某一个非终结符后面出现了哪些终结符的时候，我们需要用推出空这个产生式。

求Follow集的规则：

1.先将$放入Follow(S)中，S为开始字符。(构建LL(1)分析表的时候，如果有$S\Rightarrow\epsilon$,那么就可以写在[S,$]里，表示如果接受的是一个空串，就可以用这个产生式)

2.如果存在产生式$A\rightarrow\alpha B\beta$,那么求解Follow(B)的时候，要将$First(\beta)$中除了$\epsilon$所有的元素都加入Follow(B)。$\beta$可包含终结符或非终结符。

3.产生式右侧被推导出之后，左侧的Follow集就是右侧最右（需要考虑右侧是否为空，若为空就不断考虑向左移动的符号）的非终结符的Follow集的子集。

【如果存在产生式$A\rightarrow\alpha B\beta$,且$\beta$可空（或者说B的First集包含$\epsilon$)，那么$Follow(B)\Leftarrow Follow(A)$】

因为我们确定某个非终结符的Follow集，都是通过它在右侧才能确定的，因此我们不需要考虑那些右侧全是终结符的产生式。

LL(1)分析表做的是这件事：横轴是预测的下一个字符，然后当前的栈顶的非终结符已知，那么要通过哪一个产生式能够最终推出预测的下一个字符。所以我们需要通过计算First集和Follow集来确定LL(1)分析表。

自顶向下的语法分析

从开始符号最终到实际的字符串，自顶向下中主要分为回溯分析程序和预测分析程序。我们主要学了两种预测分析方法：递归下降和LL(1)。

为何叫“预测分析”，我们可以这么理解：首先，自顶向下分析方法的基础就是将字符串看成输入串，就是说从开始到结束，我们可以认为是逐步读取这个串的，因此字符之间有了先后被读取的，那么我们构建语法分析树也就是一个先根次序创建树的过程，我们也可以说自顶向下分析就是要找到对应串的最左推导。因此预测分析首先是要求给定的文法中没有左因子、左递归，文法不能是二义性的，其次预测分析需要看文法的下一个字符，也就是下一个输出符号，所以我们称之为“预测”。

回溯分析程序

预测分析程序

递归下降

改写为$EBNF$(消除左递归、去除左因子)

LL(1)分析算法

第一个L表示从左向右扫描输入，第二个L表示最左推导，1表示每一步中只需要向前看一个输入符号来决定语法分析动作。

预测分析表的构建

$LL(1)$构建预测分析表的步骤：

  1. $First(\alpha)$中的每个记号$s$，都将$A\rightarrow\alpha$添加至$M[A,s]$中。
  2. $\alpha$可空的话，对$Follow(A)$中的每一个元素$k$，将$A\rightarrow\alpha$添加到$M[A,k]$中。

如果$M[A,\alpha]$没有产生式的话，就将其设置为$error$。

LL(1)文法

一个文法若满足以下条件，则该文法就是LL(1)文法：

在每个产生式$A\rightarrow{\alpha}_1 |{\alpha}_2⋯|{\alpha}_n$中，对于所有的i和j:$1≤i, j≤n, i≠j$，$First(α_i )∩First(α_j )$为空。（若不为空，假设有一个相同元素$k$,那么在$M[A,k]$就会加入两个产生式：$A\rightarrow{\alpha}_i$和$A\rightarrow{\alpha}_j$)

若对于非终结符A可空，那么$First(A)∩Follow(A)$为空。(若有相同元素k，根据分析表也会发现$M[A,k]$有两个产生式)

如果一个文法G，由它构造的LL(1)分析表中的每个子项最多只含有一个产生式，那么它就是LL(1)文法。

在LL(1)分析表中有两项产生式的文法不一定是二义性的文法，可能是有左递归的。

一个不是$LL(1)$的文法同样可以用$LL(1)$方法。

LL(1）方法对应的是非递归的预测分析器，显示维护栈结构，应该和计算理论里的下推自动机类似。下推自动机所定义的语言恰好就是上下文无关语言。

自底向上的语法分析

归约其实就是推导的反向操作。如果反向构造一个推导过程，那么就会是最右推导的。推导的方法是从记号串开始，使用产生式进行归约，期望得到开始符号，如果能够得到开始符号，那么这个字符串就是文法可以识别的语句。

两个动作：移进 shift和规约 reduce。

自底向下就是从输入串到开始符号的归约，归约的方向是从左到右，可以认为是最左归约，逆向的过程就是最右推导。

概念

短语、直接短语和句柄

短语就是在一个句型中对应的分析树，里以非终结符为根的子树的所有叶子节点构成的排列就是对于该非终结符的短语，如果子树只有两层，那么就是直接短语。最左侧的非终结符的子树对应的短语就是句柄。

句柄的定义：如果$S\Rightarrow_{lm}^{*}\alpha A\omega \Rightarrow_{lm} \alpha \beta \omega$，A是输入串中最右的非终结符，则$\beta$称为一个句柄。

句柄可以理解为一个归约点，可以允许解析器通过进一步的归约操作回到开始符号的位置。而实际上我们做的归约就是最左归约。

对于下列文法：

$E\rightarrow E+T|T$
$T\rightarrow T*F|F$
$F\rightarrow (E) |id$

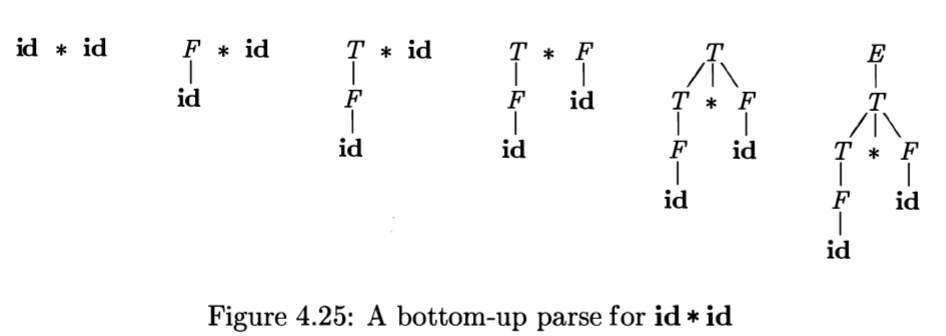
对于输入串$id*id$，从左到右相当于一个最左归约的过程。从左至右：

产生式 句柄 最右句型
$F\rightarrow id$ $id$ id*id
$T\rightarrow F$ $F$ F*id
$F\rightarrow id $ $id$ T*id
$T\rightarrow T*F$ $T*F$ T*F
$E\rightarrow T$ $T$ T

image-20200521195029382

可行前缀

LR(0)分析算法

LR(0)文法中L指的是从左到右扫描输入串，R代表了最右推导，0表示进行分析动作的决策只考虑栈顶状态，不需要看输入串。（没有lookahead)

1.扩展文法。

在决定状态间的转移前，我们必须先加入一条扩展文法：$S\rightarrow E$其中$S$是新的起始符号（start symbol）而E是原先的起始符号。这一做法是为了保证分析器能有一个唯一的起始状态。

2.列LR(0)项。(点号的左侧是已经读入的，点号的剩余是还没有读入的)

3.起始状态是所有点在最左侧的LR(0)项组成的封闭集,构建LR(0)自动机

4.构建LR(0)分析表。

5.进行分析。

如果X是终结符，只要有移进项先移进。

LR(0)文法

无歧义需要没有归约归约冲突或移进归约冲突。

SLR(1)分析算法

如果当前栈顶状态可以支持终结符移进，并且下一个记号也就是该终结符，才会移进。如果当前栈顶状态包含了归约项$A\rightarrow\gamma.$，且下一个记号在$Follow（A)$时，才会使用$A\rightarrow\gamma$归约，如果不在$Follow(A)$也不会做归约。$GOTO$项与LR(0)类似。

歧义的产生：

1)有归约项和移进项，且移进项$A\rightarrow \alpha . X \beta$的下一个字符$X$在$Follow（B）$中,当然如果下一个记号不是$X$那么就没有歧义了。

2)有两个不同的归约项$A\rightarrow\beta.$，$B\rightarrow\gamma.$，且下一个记号即在A的Follow集也在B的Follow集，或者两个Follow集都没有$X$,此时要报错。

当确认没有歧义的时候，归约项$r(A\rightarrow \gamma)$就会被填入A的Follow集对应的Input下。