[toc]

Neural Machine Translation(NMT)

Neural Machine Translation,简称NMT, 是指使用深度学习来完成机器翻译任务。NMT任务是一个端到端的学习任务，输入一个序列直接输出对应的目标序列。如图1所示，模型输入句子“ABC<EOS>”, 输出对应的翻译句子“WXYZ<EOS>”，该图可以分为两个部分：编码（encode）和解码（decode）。

图1 （图片来源：Sutskever et al.2014）

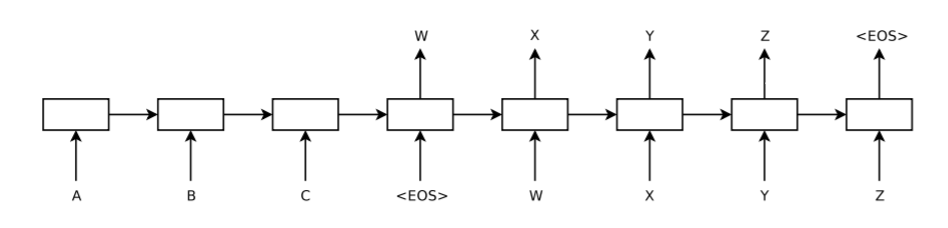
左侧encoder输入”ABC<EOS>“，右侧decoder逐个预测出翻译的单词。decoder并不能直接确定预测单词的个数（句子的长度），预测的结束以通过预测到<EOS>结束，当decoder输入Z时，模型预测出<EOS>字符（end-of-sentence)，表示预测结束。

Seq2seq模型

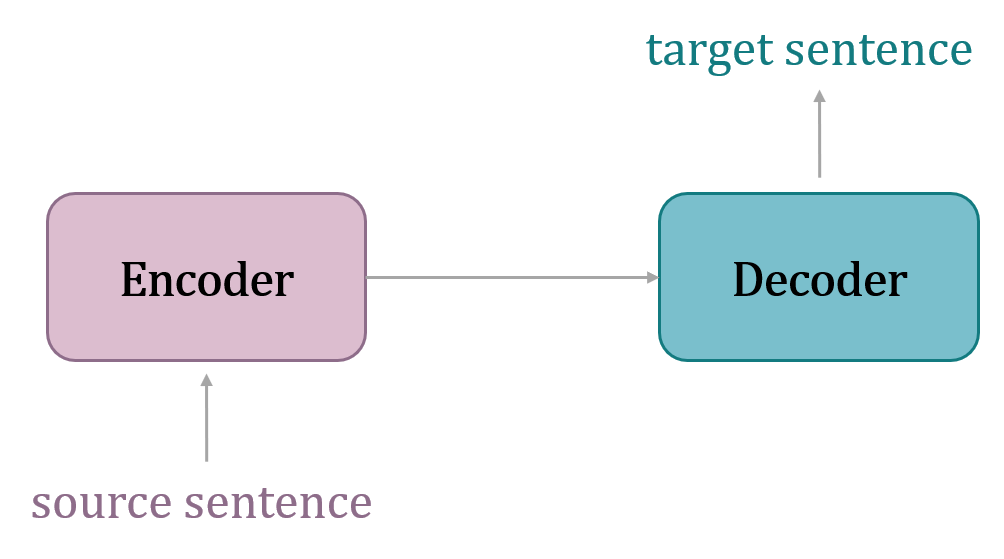
整个框架也被称为Sequence-to-sequence模型（简称为Seq2seq），是一种使用RNN结构来解决NLP相关的问题的模型。最早由 (Sutskever et al.,2014)提出，该方法是基于encoder-decoder框架下使用LSTM对文本进行翻译。encoder-decoder框架是sequence-to-sequence任务中的一个标准的模型，如图2。

图2 encoder-decoder框架

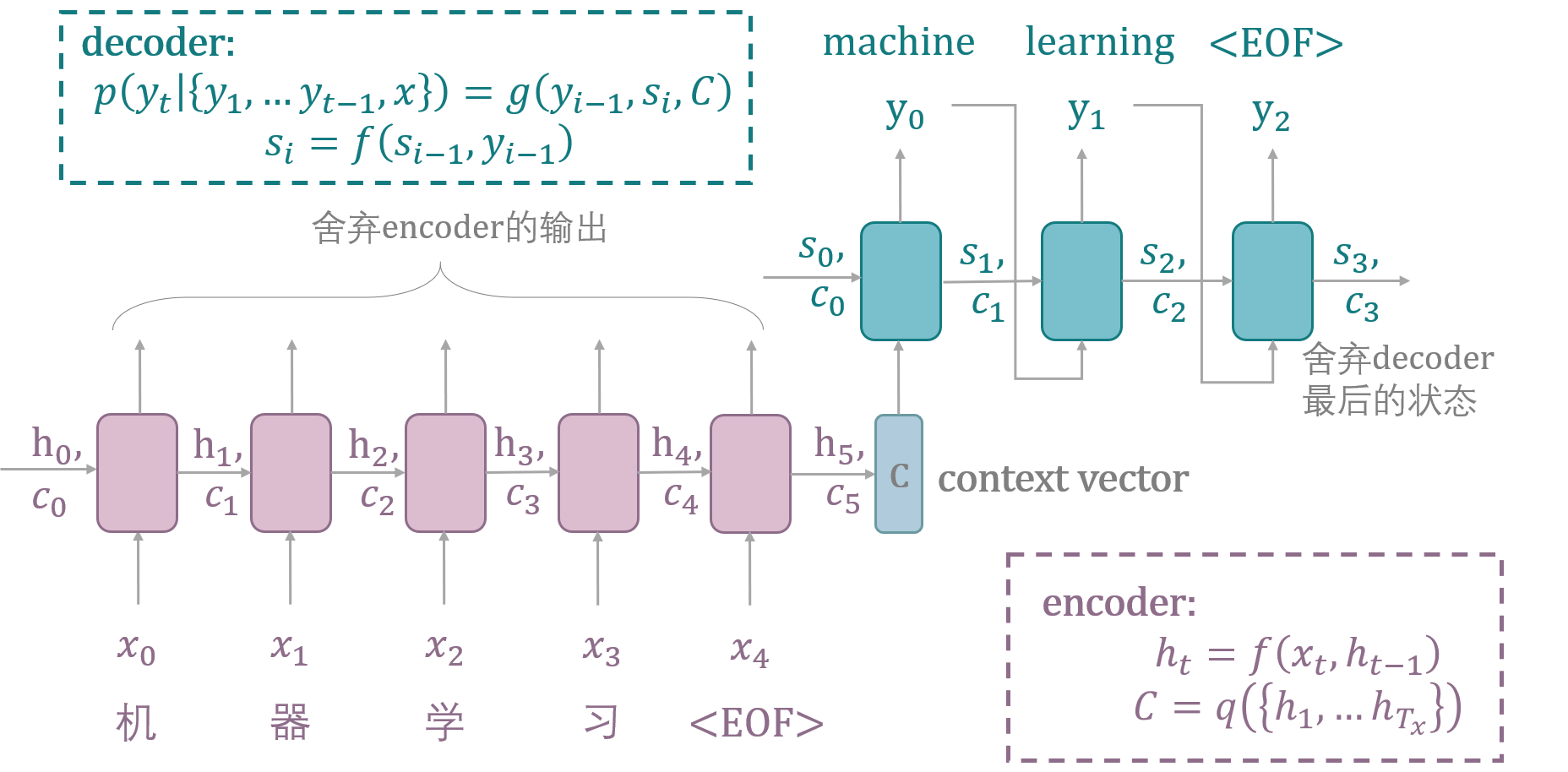
encoder和decoder通常都是RNN单元，如LSTM模型或GRU模型。encoder读入原始的序列，生成整个输入序列的representation（即上下文向量context vector），其中encoder的输出会被丢弃，只有隐藏状态（hidden state）会被保留。

decoder使用encoder输出的representation，生成目标序列。decoder的初始状态由encoder的最后一个LSTM单元的最终状态进行初始化。每一个LSTM单元都会接受上一个单元的隐藏状态，并生成自己的隐藏状态作为输出。

图3 Seq2seq模型原理图

encoder

如图3，在编码阶段，模型输入语句 $x=(x_1,…x_{T_x})$ ，使用RNN计算上下文向量（context vector），其中t时刻的隐含状态计算公式如下：
$$
h_t=f(x_t,h_{t-1})
$$
通过encoder，能够用隐含状态计算出输入语句的embedding，也被称为上下文向量（context vector)，记作$C$：
$$
C=q({h_1,…h_{T_x}})
$$
其中$f$和$q$是两个非线性函数， (Sutskever et al.,2014)使用LSTM作为$f$, $q({h_1,…h_T })= h_T$作为$q$，即将最后一个隐藏状态$h_T$作为上下文向量。

decoder

如图3，在解码阶段，模型逐个预测单词。当预测单词$y_{t^{‘}}$时，给定的上下文向量$C$和所有之前预测的单词${y_1,…y_{t^{‘}-1}}$将会用于预测。decoder生成的目标序列$y=(y_1,…y_{T_y})$，条件概率为：
$$
p(y)=\prod_{t=1}^{T}p(y_t│{y_1,…y_{t-1}},C)
$$

最终decoder确定最终预测的单词是概率向量中概率最大的词。
$$
y_{t^{‘}}=arg\mathop{max}\limits_{y}p(y|x)=arg\mathop{max}\limits_{y}\prod_{t=1}^{T}p(y_t│y_{<t},x)
$$
当decoder使用RNN，则条件概率可以被表示为$p(y_t│y_1,…y_{t-1},C)=g(y_{t-1},s_t,C)$，其中$g$也是一个非线性的多层函数。decoder的第$t$个单元生成的隐含状态$s_t$和前一个单元的输出$y_{t-1}$作为输入，生成当前单元的输出$y_t$的概率向量。

decoder还会使用”Teacher Forcing”提高训练的效率，此处不展开介绍，可以参考这篇文章。

Seq2seq的问题

  1. Seq2seq模型中context vector是一个固定的向量，将输入的整句话编码成固定尺寸的向量，可能会损失句子的信息，限制模型的性能。
  2. 对RNN结构来说，序列长度越长，神经网络越深，这将导致梯度消失，结构的效果会有所下降。尽管LSTM可以一定程度上防止该问题，但仍然有可能出现长程梯度消失问题。

Attention in NMT

为了解决Seq2seq模型存在的问题，（Bahdanau et al.,2015）将attention思想最早由运用在NMT任务中。简单地说，注意力可以被解释为一个权重向量，这个向量能够被用来估计被预测的元素（如句子中的一个单词）和其他元素的相关性。元素通过注意力向量加权和会被作为目标的近似值。网络中的注意力部分会从输入序列中映射出重要的和相关性高的词，赋予这些词更高的权重，从而提高预测的准确性。（Bahdanau et al.,2015）论文整体的框架如图4所示，这种attention机制通常也被称为Additive Attention，它保证了encoder不需要将所有的原始语句都编码为一个固定长度的向量。

图4 模型框架（图片来源：Bahdanau et al.,2015）

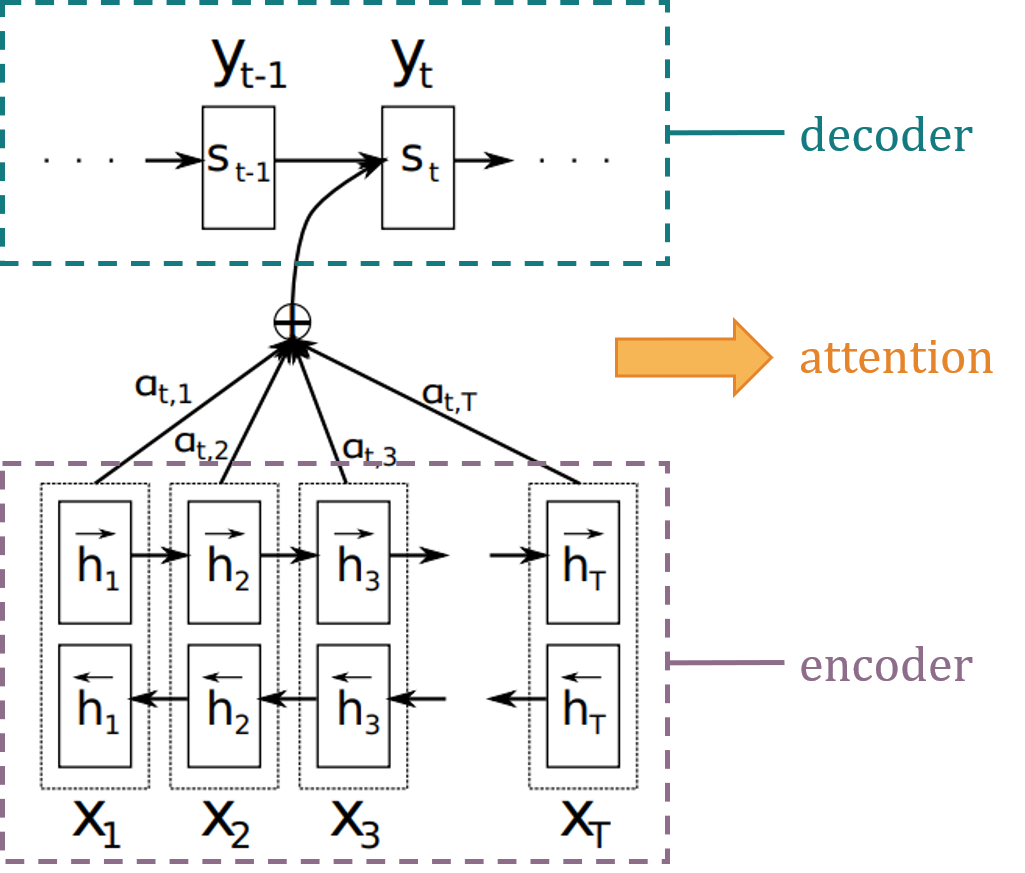
encoder：BiRNN

在encoder部分，使用的是一个双向的RNN（BiRNN），会生成一个前向的隐藏状态序列和后向的隐藏状态序列，将前向和后向对应的状态进行连接（concate），BiRNN使得每一个$h_j$都包含之前和之后单词的信息。

图5 双向RNN原理

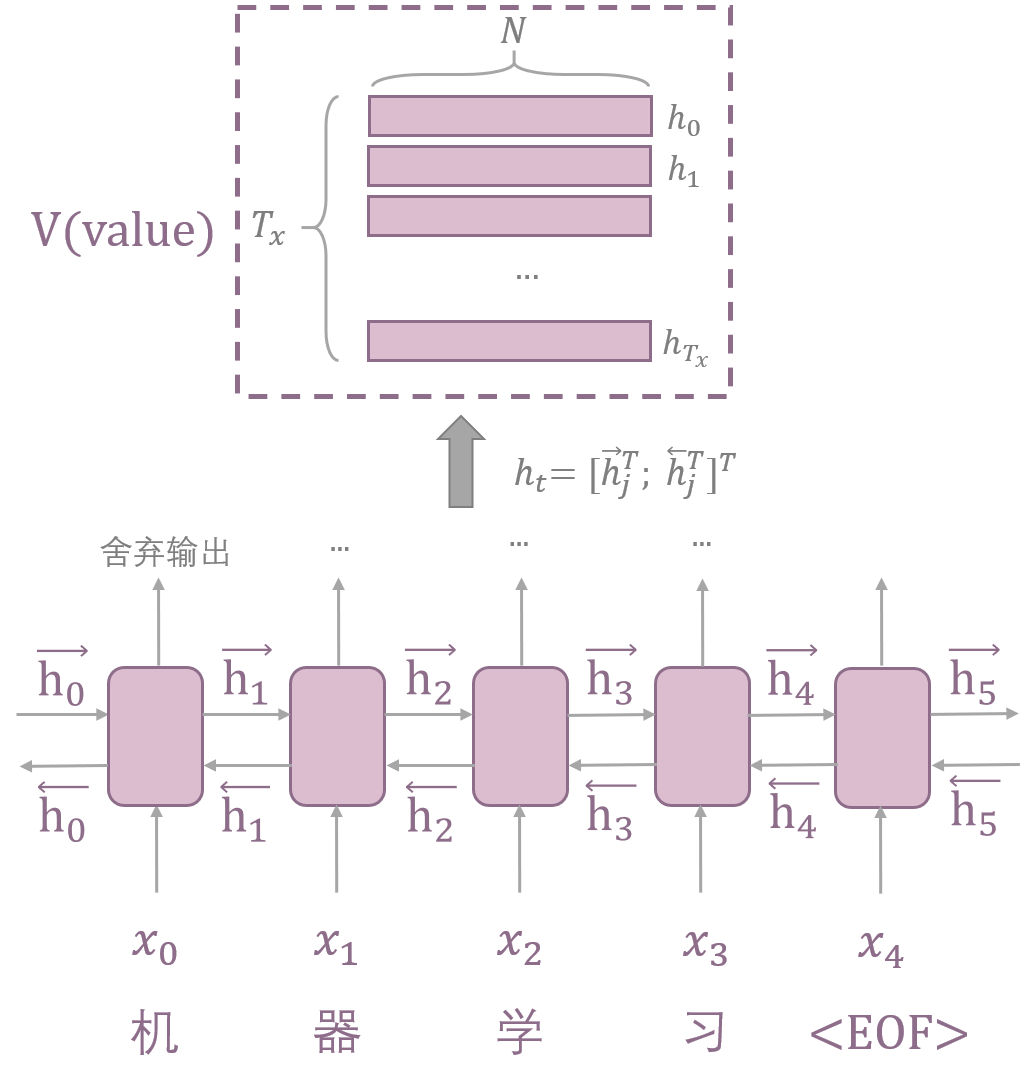
Seq2seq模型中，encoder产生的最后一个状态将作为context vector，与Seq2seq不同的是，这里encoder产生的每一个状态都将在decoder用于计算context vector，且context vector成为了一个动态的表示。

decoder：Additive Attention

实际上，在Additive Attention中，context vector的计算需要利用encoder和decoder产生的状态，具体的流程如下图所示：

图6 如何计算context vector

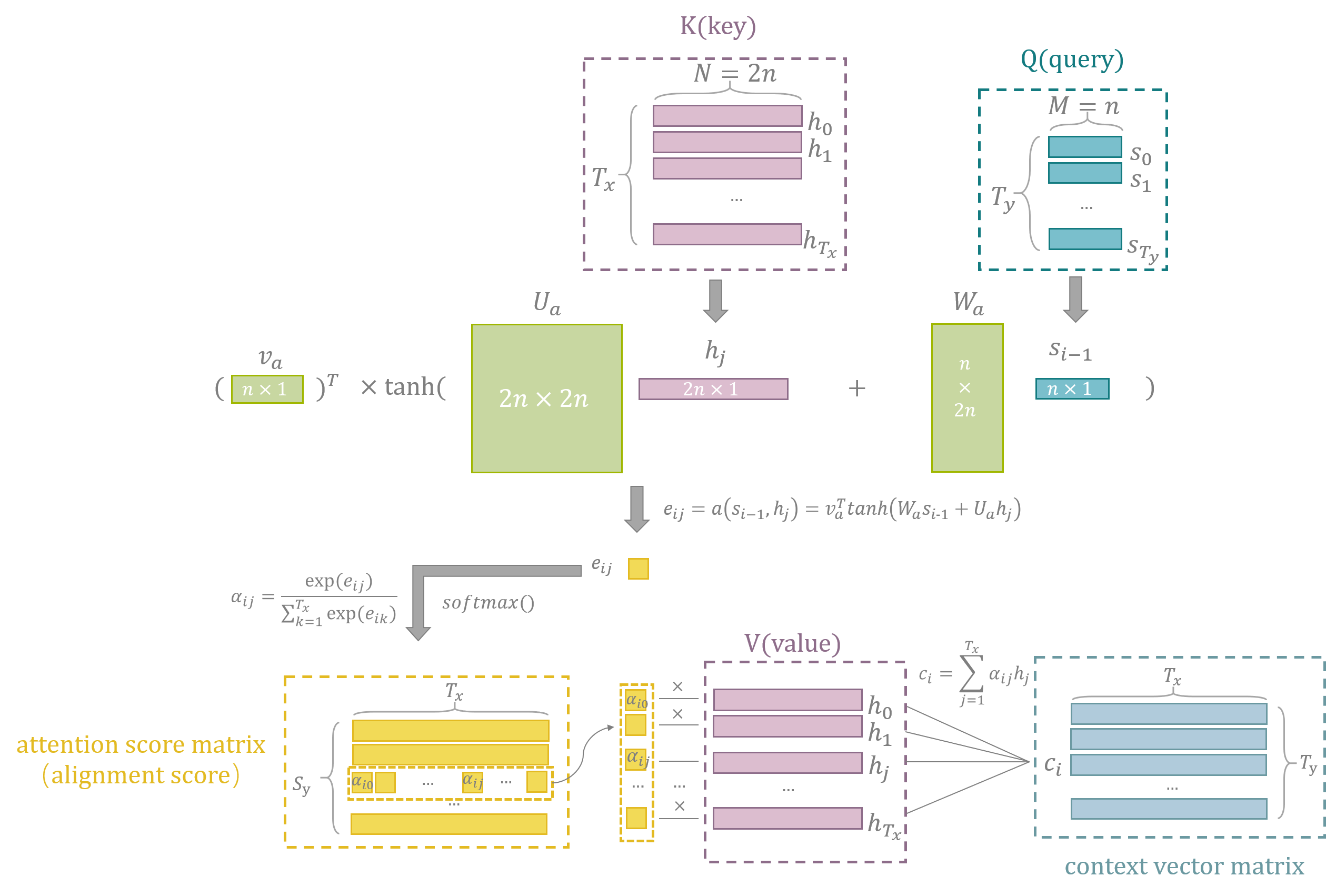
在decoder中，条件概率被定义为：
$$
p(y_t│y_1,…y_{t-1},x)=g(y_{i-1},s_i,c_i)
$$
$s_i$是decoder中RNN的第$i$隐藏状态，$s_i=f(s_{i-1},y_{i-1},c_i)$，如图6，$s_i$的计算需要：1）上一个隐藏状态$s_i$，2）上一个单元生成的$y_{i-1}$,3)由上一个隐藏状态计算出的当前的上下文向量$c_i$。这里和seq2seq模型的区别是，seq2seq仅会产生一个上下文向量$c$，但通过attention机制会生成多个上下文向量。每个上下文向量由encoder的隐藏状态的加权和计算得出：
$$
c_i=\Sigma_{j=1}^{T_x}\alpha_{ij}h_j
$$
这个值相当于计算所有的状态的期望。$\alpha_{ij}$表示$i$时刻第$j$个状态的权重，这个权重可以被理解成目标语言生成的$y_i$能够翻译源语言的单词$x_j$的概率，$\alpha_{ij}$也可以被称为attention score，计算公式为：
$$
\alpha_{ij}=\frac{exp⁡(e_{ij})}{\Sigma_{k=1}^{T_x}exp⁡(e_{ik})}
$$

这个式子说明$\alpha_{ij}$其实就是$e_{ij}$的softmax值，$e_{ij}$相当于一个分数，表示输入$j$位置和输出的$i$位置的匹配程度，计算公式为：
$$
e_{ij}=a(s_{i-1},h_j)=v_a^Ttanh(W_as_{i-1}+U_ah_j)
$$
$a$表示一个alignment model，通过feedforward神经网络进行训练，$W_a\in R^{n\times n}$，$U_a\in R^{n\times 2n}$和$v_a\in R^n$都是权重矩阵。$U_ah_j$可以被预先计算出来。

关于alignment：

alignment在NMT中，指的就是不同种的语言单词语义上的相近，如机器学习翻译为machine learning，机器和machine在语义上是等价的，这就是一种alignment。alignment也可以理解为correspondence，以翻译文本为例，除了一对一的alignment，还可能会出现多对一、一对多的alignment。

soft alignment和hard alignment：（Bahdanau et al.,2015）使用的加权矩阵就可以被称为attention soft-alignment matrix,基本上可以把attention机制理解成soft alignment。

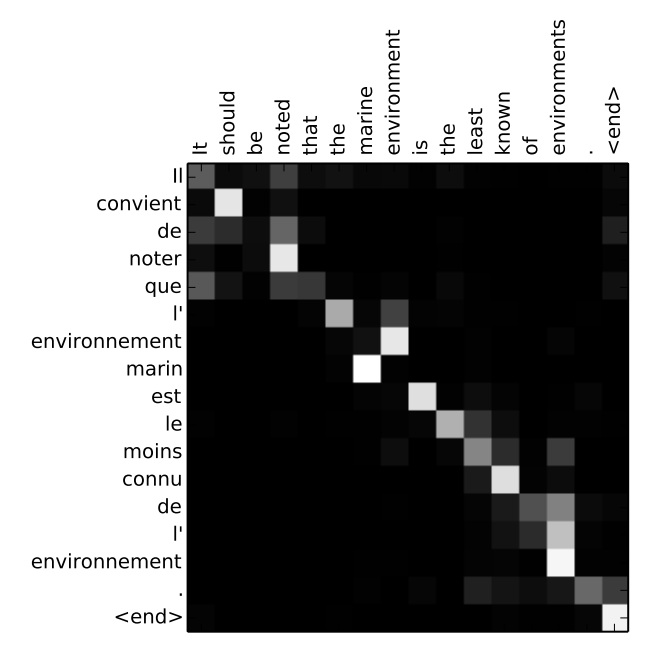
下图表示翻译句子时的alignment scores matrix，灰度颜色越浅表示source word和target word的相关度越高（alignment score越大）。在这个图中能够看到在生成target word时，哪些source word更重要。

图7 alignment scores matrix（图片来源：Bahdanau et al.,2015）

Q(query)、V(values)和K(keys)

用QKV的视角来理解attention最早是在（Vaswani et al.,2017）中，在图6，标注了计算context vector过程中参与计算的Q、K、V矩阵。

values/keys: 把编码好的输入的表示看成key-value pairs$(K,V)$ ,长度为N, key和value皆是encoder的隐藏状态。

query：在decoder阶段，之前的输出会被压缩成一个query$(Q)$,长度为M。decoder的输出用于映射这个query和key-value pairs的集合。模型decoder会输出一个word的distribution, query就是最有可能的单词的表示向量。

Attention Family

图8 Attention Family

soft&hard attention

attention机制在NLP领域被提出后，很快被应用到了CV领域(Xu et al. 2015)。在这篇文章中，首次提出了soft attention和hard attention的概念。

soft attention指相对“柔和地”利用attention score来加权计算context vector，相当于求的是context vector的期望。（Bahdanau et al.,2015）中提出的模型就是soft attention。hard attention是将context vector看做随机变量，context vector的取值是利用参数为attention score的多项式分布在value中进行采样获得的。下图是(Xu et al. 2015)中两种attention机制的实验中的attention矩阵的可视化，通过下图能够直观地理解soft attention和hard attention的区别。

图9 Attention的可视化（图片来源：Xu et al.,2015）

soft attention是differentiable的，但当输入较长的时候模型代价较大，hard attention在预测时需要的计算更少，但模型是non-differentiable的，在训练时需要更多的技巧。

global&local attention

根据计算context vector时利用encoder的隐藏状态的多少，可以分为global attention和local attention（Luong et al.,2015）。

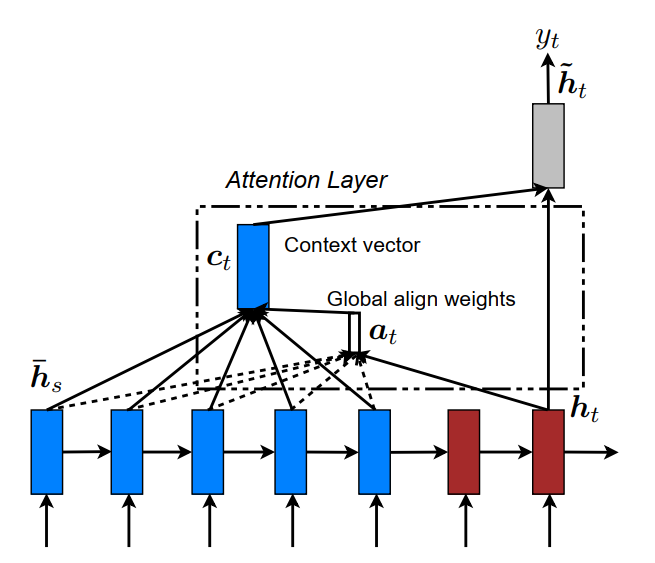
global attention

global attention的原理和（Bahdanau et al.,2015）较为相似，其中不同的部分是：

1.在计算$score(s_i,h_j)$时，将$s_i$和$h_j$直接进行concat。

2.简化了计算过程：$h_t \rightarrow a_t \rightarrow c_t \rightarrow \widetilde h_t$ （Bahdanau et al.,2015的计算过程为$h_{t-1} \rightarrow a_t \rightarrow c_t \rightarrow h_t$ ）。

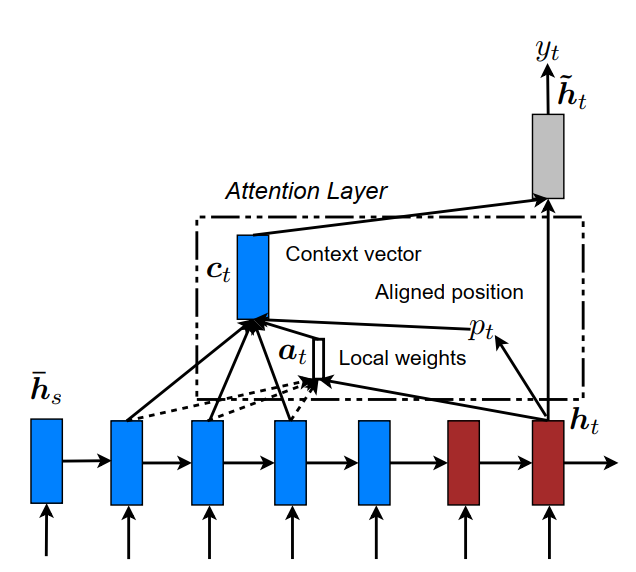
图10 global attention原理（图片来源：Luong et al.,2015）

local attention

local attention的引入是为了解决global attention中复杂度较高的问题。local attention会根据目标词的隐藏状态$h_t$计算出相应的对齐位置$p_t$，context vector的计算是通过$[p_t-D,p_t+D]$区间内的encoder中的隐含状态的加权和来进行计算的。D是根据经验选择的。
$$
p_t=S \times sigmoid(v_p^T tanh(W_ph_t))
$$
$S$是原序列的长度，以$p_t$为中心的高斯核函数进行衰减，aligned weights被定义为：
$$
a_t(s)=align(h_t,\overline h_s)exp(-\frac{(s-p_t)^2}{2\sigma^2})
$$
其中，$\sigma=\frac{D}{2}$。

图11 local attention原理（图片来源：Luong et al.,2015）

当前对目标单词的预测值，没有利用已经预测的输出单词（encoder的隐藏状态）作为输入，也没有利用目标词位置前一时刻的decoder隐状态$h_{t−1}$，仅利用了当前decoder的隐藏状态$h_t$来计算。说明每个目标单词的决策是独立的。

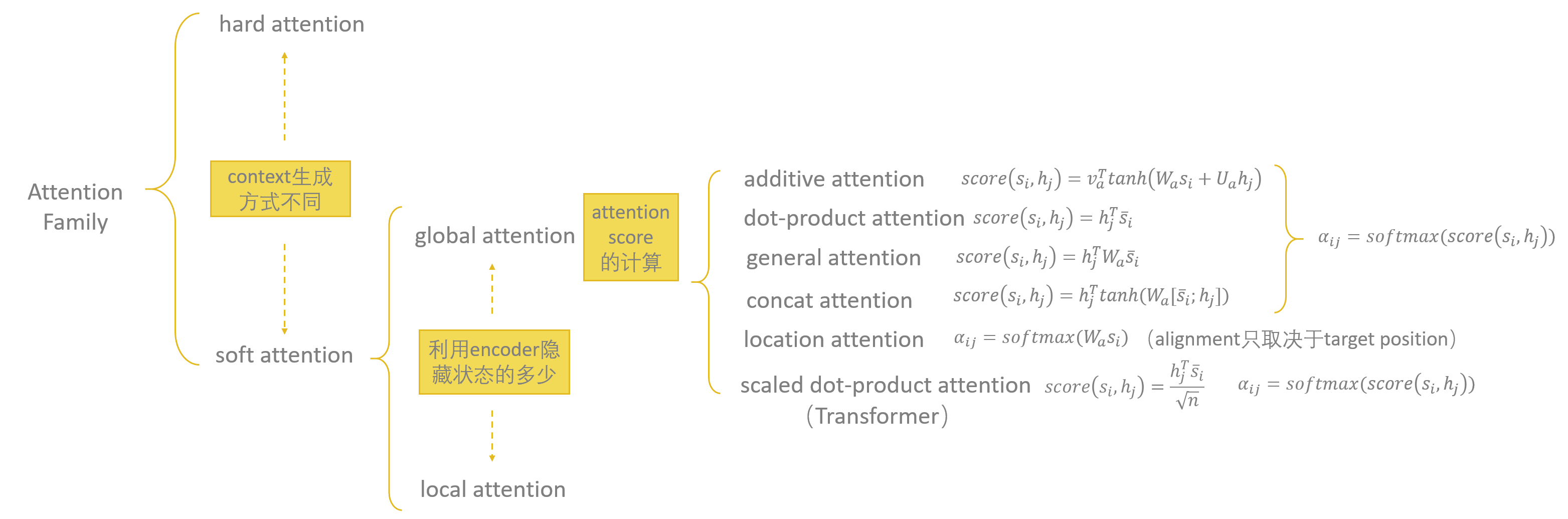
attention score不同的计算方式

根据attention score计算方式的不同，有如下的attention机制：

不同的attention score具体计算方式图8所示。

Self-Attention

自注意力机制和普通的注意力机制的区别在于，自注意力机制考虑的是输入元素（source word）之间的相关性，而非输入元素和输出元素之间的相关性（source word和target word），因此，自注意力机制能够使用上述任意一种attention score的计算方式，只是其目标序列和输入的原始序列相同。我们可以把它理解成一个全连接层，权重是由输入的成对关系动态生成的。

关于self-attention具体的原理和Query、Value和Keys的进一步解释，将在后续介绍Transformer的文章中展开介绍。

参考文献

[1] Sutskever, Ilya, Oriol Vinyals, and Quoc V. Le. “Sequence to sequence learning with neural networks.” Advances in neural information processing systems. 2014.

[2] Bahdanau, Dzmitry, Kyunghyun Cho, and Yoshua Bengio. “Neural machine translation by jointly learning to align and translate.” ICLR. 2015.

[3] Minh-Thang Luong, Hieu Pham, and Christopher D. Manning. “Effective Approaches to Attention-based Neural Machine Translation.” EMNLP. 2015.

[4] Yang, Shuoheng, Yuxin Wang, and Xiaowen Chu. “A survey of deep learning techniques for neural machine translation.” arXiv preprint arXiv:2002.07526 (2020).

[5]Xu, Kelvin, et al. “Show, attend and tell: Neural image caption generation with visual attention.” International conference on machine learning. PMLR, 2015.

[6] Ashish Vaswani, et al. “Attention is all you need.” NIPS,2017.