Transformer Family

[toc]

Transformer基础结构

图1 Transformer基础结构

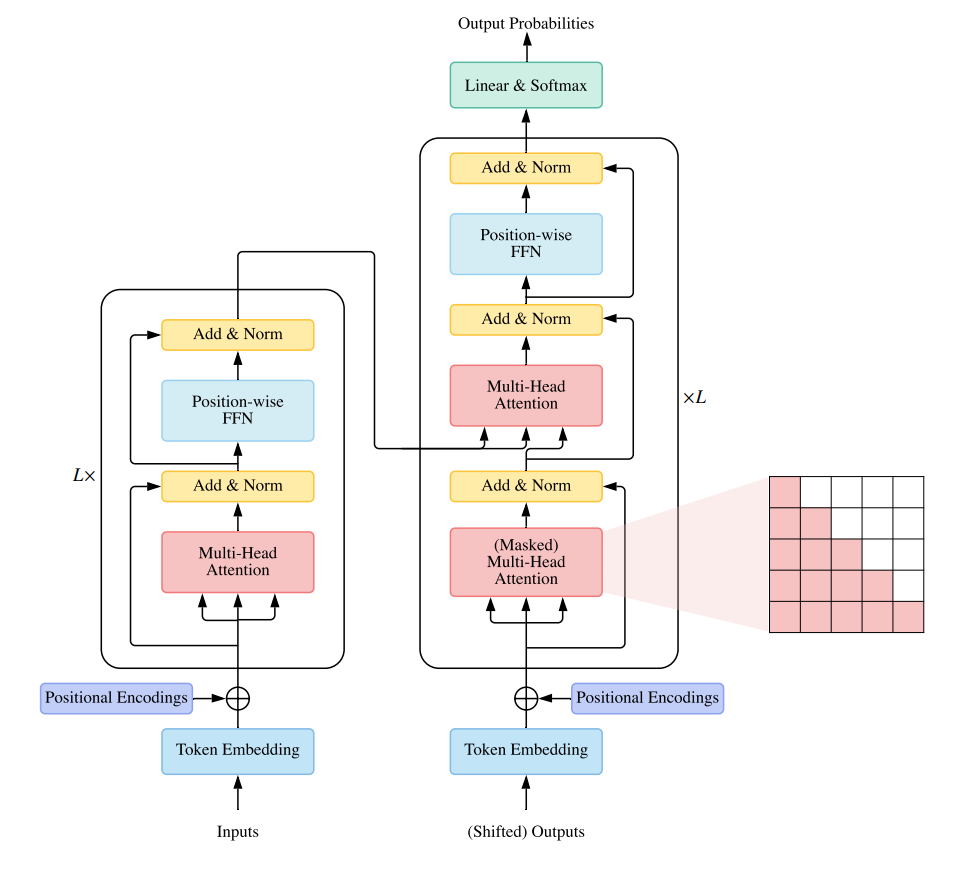
综述总结

A Survey of Transformers (2021)

分类方法：分四个部分进行分类：model-level、arch-level、pre-train model、application。

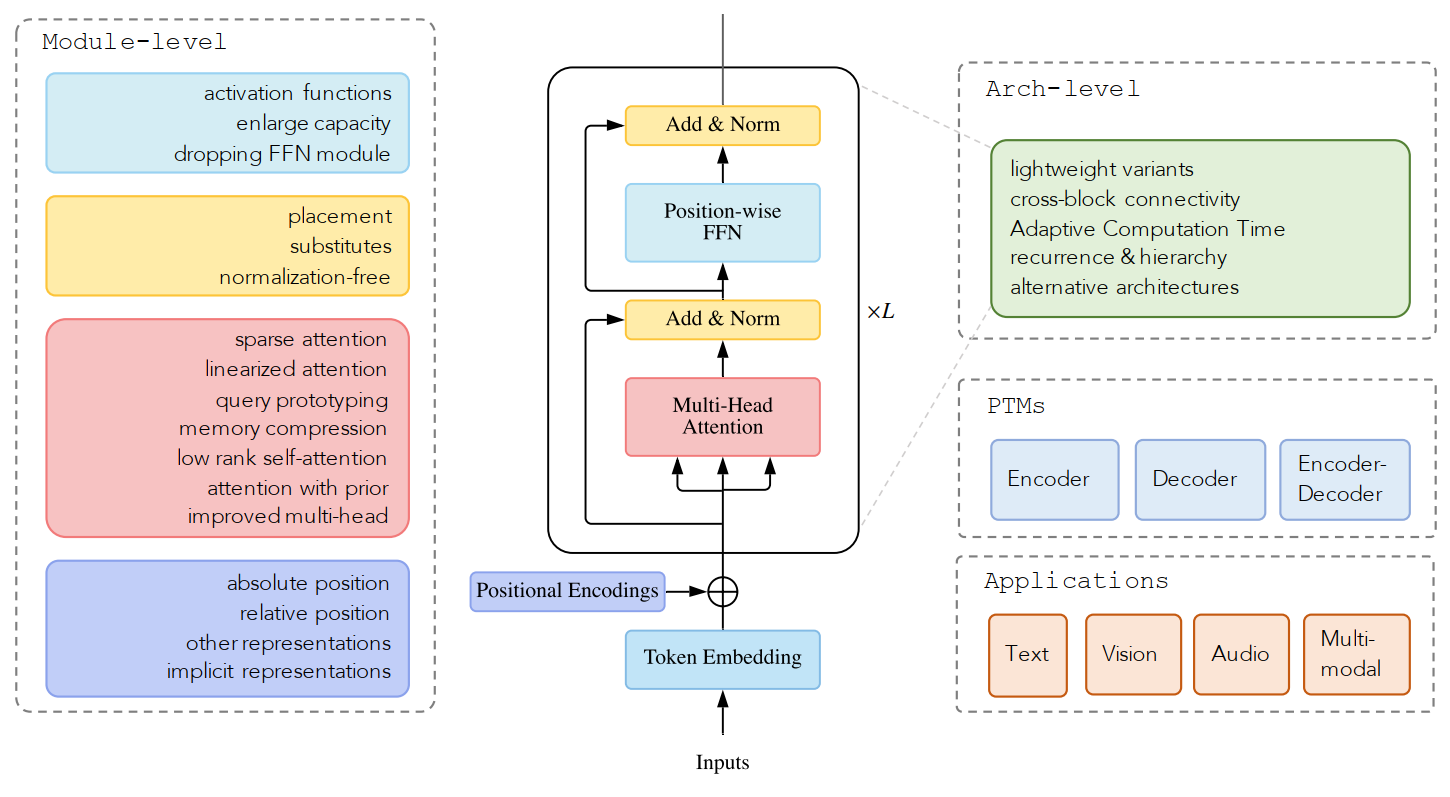
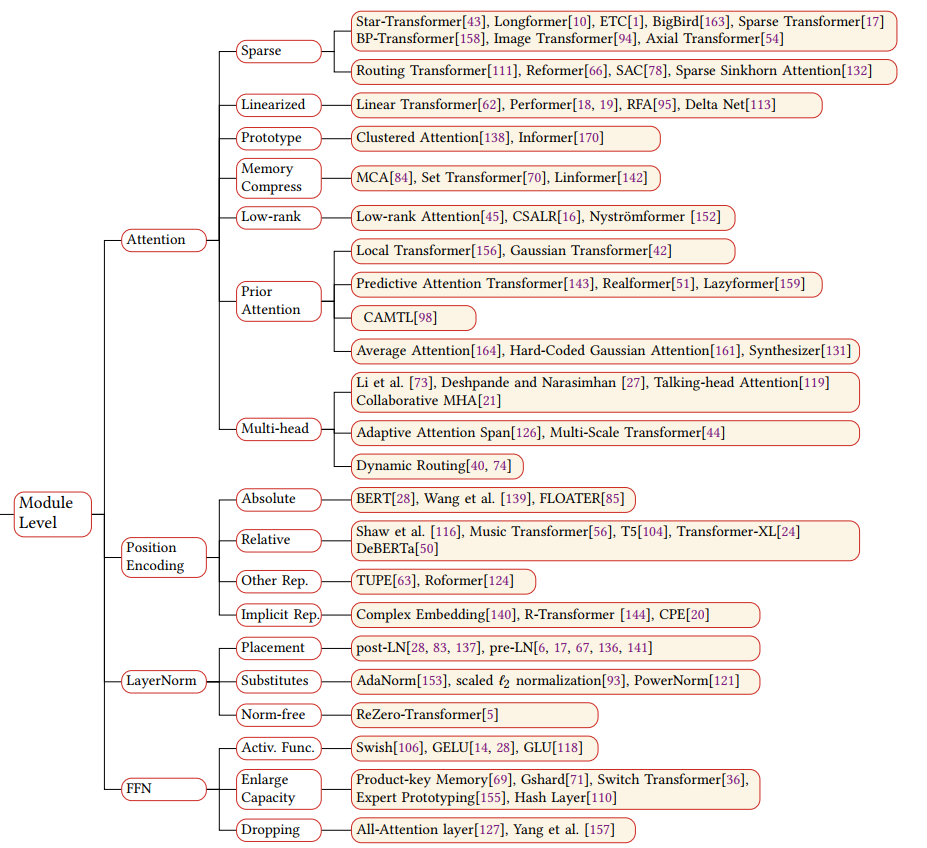
图2.Transformer分类1

model level：

图3 Transformer方法模型层面的分类

architecture level:

图4 Transformer方法架构层面的分类

pre-Train:

图5 Transformer方法不同预训练的分类

App:

图6 Transformer方法的应用分类

Efficient Transformers: A Survey (2020)

分类方式：考虑Transformer如何提高其计算和内存的效率，分为五种不同的方法。

图7 Transformer分类2

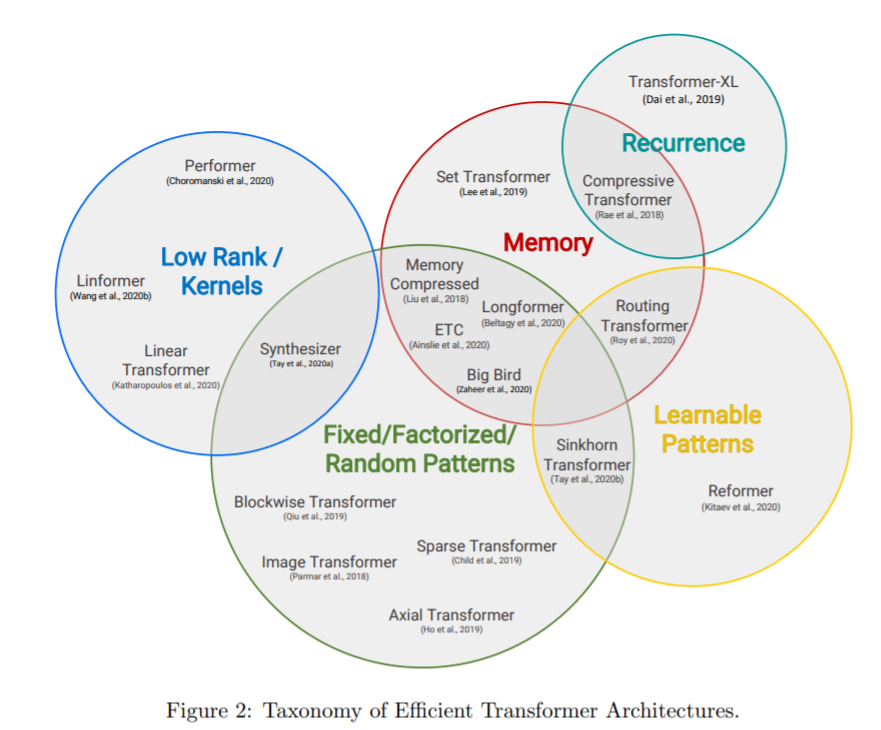
1. Fixed patterns(FP)：Sparse Transformer

通过限制attention的范围(从全局变成局部)来降低计算复杂度。限制范围的方法包括blockwise pattern，strided pattern，compressed pattern。

Blockwise pattern：将输入序列切成多个block，attention只发生在block范围内，所以复杂度从$O(N^2)$降到$O(B^2)$，B为block size，但是这样切割会导致序列不连贯，attention能力受限。

Strided pattern：采用滑动窗口的形式，每个token与周围相邻的几个token作attention，相邻的token范围就是window size，这样是有一定道理的，因为自然语言在多数情况下都是局部相关的，所以在一个窗口范围内作attention往往不会丢失太多信息，相比之前的blockwise pattern。（Sparse Transformer)

Compressed pattern：先通过卷积池化对序列进行降采样，比如用核为2，步长为2的CNN，将2个token表征成一个向量，然后再做attention，同样也能降低attention的计算复杂度。相当于通过CNN对序列进行n-gram的切分。

2、Learnable patterns(LP) ： Reformer

fixed pattern是认为规定好一些区域，让该区域的token进行注意力计算，而Learnable patterns则是通过引入可学习参数，让模型自己找到划分区域。Reformer引入基于哈希的相似度度量方法将输入序列切割。所以本质上说LP与FP是一致的，都是通过将整体序列切分成子序列，attention只在子序列中进行，从而降低计算开销，只不过LP的区域划分是通过模型学得，而FP则是人为定义。

3、Memory： Compressive Transformer、Set transformer

在压缩编码解码的过程中肯定会有信息损失，一种改进方法是引入global memory，包括了之前输入序列token的信息。memory可以与所有的token进行注意力交互,由于这些token的数目远小于序列长度，因此也不会给计算带来负担，而且往往携带了整个输入序列的信息。

4、Low rank methods ：Linear Transformer、 Linformer、Performer

关于注意力矩阵的低秩表示，在Linformer论文中有详细的论述。简单来说， 经过softmax之后的$N\times N$的注意力矩阵是不满秩的，这意味着我们不需要计算一个完整的注意力矩阵，因此我们可以将 $n \times d$ 维（n表示序列长度，d表示模型向量维度）的$K，V$向量映射到$k \times d$ 维空间。

5、Kernels ：Linear Transformer

以核函数变换的新形式取代原有的softmax注意力矩阵计算，将计算复杂度降至$O(n)$ 范围内。

6、Recurrence ：Linear Transformer、 Transformer-XL

recurrence实际上也是fixed patterns中blockwise的一种延伸。本质上仍是对输入序列进行区域划分，不过它进一步的对划分后的block做了一层循环连接，通过这样的层级关系就可以把一个长序列的输入进行更好的表征。

1. Transformer-XL（ACL 2019）

标准Transformer有一个固定有限的attention范围。在每一个更新的步中，模型只能够处理同一segment中的其他元素，信息无法在分离的segment中传递，也就意味着Transformer很难捕捉长期的依赖关系，在上下文较短的情况下，难以进行预测。

Transformer-XL (Dai et al., 2019)进行了如下的改进：重用segment之间的隐藏状态，采用新的适合重用状态的位置编码。

隐藏状态重用

Transformer-XL通过连续使用前一个segment的隐藏状态，将segment之间的递归引入到模型中。如下图，一个segment的长度为4，可以看出Transformer和Transformer-XL的区别。

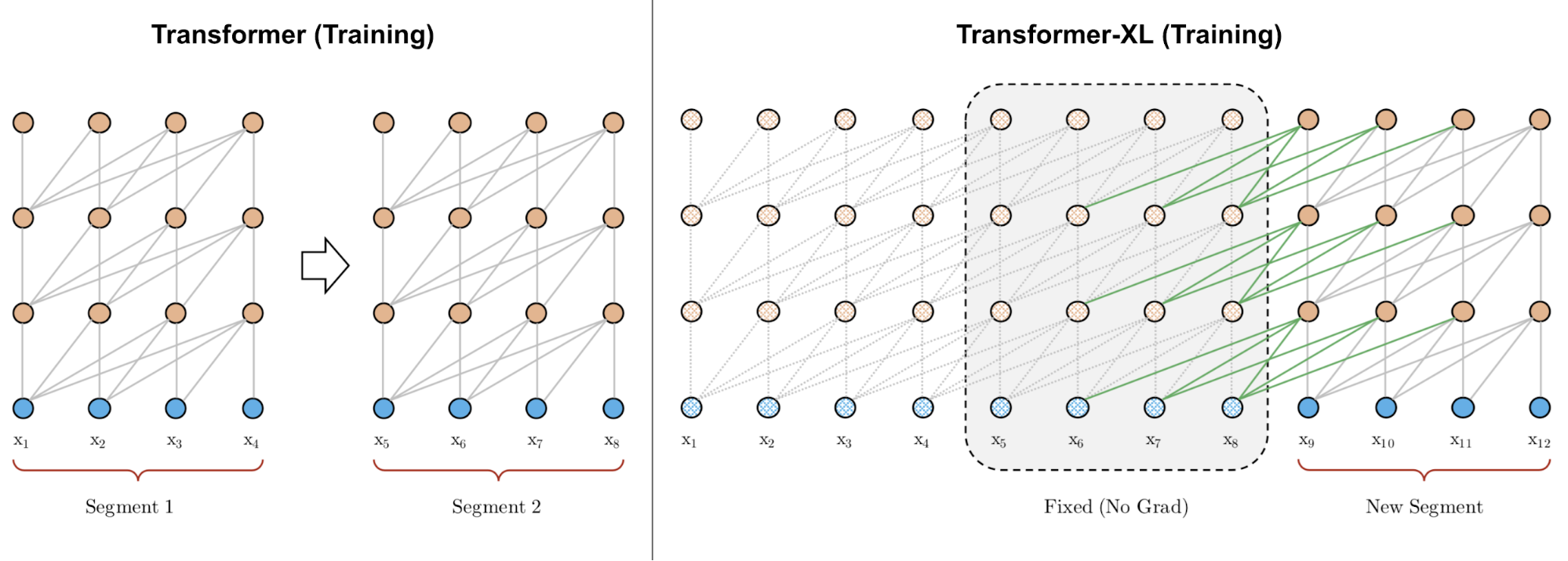
图8 Transformer和Transformer-XL的对比（图片来源：Dai et al.,2019）

第$(\tau + 1)$段的第n层的隐藏状态记为 $\mathbf{h}{\tau+1}^{(n)} \in \mathbb{R}^{L \times d}$，第n-1层的隐藏状态为 $\mathbf{h}{\tau+1}^{(n-1)}$。前一个段的第n层隐藏状态为$\mathbf{h}_{\tau}^{(n)}$，模型有如下的公式，通过合并之前的隐藏状态的信息，实现注意力范围的延长。

$$
\begin{aligned} {\widetilde{\mathbf{h}}{\tau+1}^{(n-1)}} &= [\text{stop-gradient}(\mathbf{h}{\tau}^{(n-1)}) \circ \mathbf{h}{\tau+1}^{(n-1)}] \ \mathbf{Q}{\tau+1}^{(n)} &= \mathbf{h}{\tau+1}^{(n-1)}\mathbf{W}^q \ \mathbf{K}{\tau+1}^{(n)} &= {\widetilde{\mathbf{h}}{\tau+1}^{(n-1)}} \mathbf{W}^k \ \mathbf{V}{\tau+1}^{(n)} &= {\widetilde{\mathbf{h}}{\tau+1}^{(n-1)}} \mathbf{W}^v \ \mathbf{h}{\tau+1}^{(n)} &= \text{transformer-layer}(\mathbf{Q}{\tau+1}^{(n)}, \mathbf{K}{\tau+1}^{(n)}, \mathbf{V}_{\tau+1}^{(n)}) \end{aligned}
$$
key和value都依赖于扩展后的隐藏状态，而query只依赖于当前的隐藏状态。

相对位置编码

Transformer-XL提出了一种新的位置编码来适应隐藏状态重用。在基础的Transformer中，编码绝对位置的话，前一段和当前段将会被相同的编码。在Transformer-XL中并不需要。为了保持段之间的位置信息的流动，Transformer-XL提出了相对位置编码，它只要知道位置的偏移量就可以做出预测。

$i$位置的query和$j$位置的key的attention score为：

$$
\begin{aligned} a_{ij} &= \mathbf{q}_i {\mathbf{k}_j}^\top = (\mathbf{x}_i + \mathbf{p}_i)\mathbf{W}^q ((\mathbf{x}_j + \mathbf{p}_j)\mathbf{W}^k)^\top \ &= \mathbf{x}_i\mathbf{W}^q {\mathbf{W}^k}^\top\mathbf{x}_j^\top + \mathbf{x}_i\mathbf{W}^q {\mathbf{W}^k}^\top\mathbf{p}_j^\top + \mathbf{p}_i\mathbf{W}^q {\mathbf{W}^k}^\top\mathbf{x}_j^\top + \mathbf{p}_i\mathbf{W}^q {\mathbf{W}^k}^\top\mathbf{p}_j^\top \end{aligned}
$$

整理可得：

$$
a_{ij}^\text{rel} = \underbrace{ \mathbf{x}i\mathbf{W}^q { {\mathbf{W}_E^k}^\top } \mathbf{x}_j^\top }_\text{content-based addressing} + \underbrace{ \mathbf{x}_i\mathbf{W}^q { {\mathbf{W}_R^k}^\top } {\mathbf{r}{i-j}^\top} }\text{content-dependent positional bias} + \underbrace{ {\mathbf{u}} { {\mathbf{W}_E^k}^\top } \mathbf{x}_j^\top }_\text{global content bias} + \underbrace{ {\mathbf{v}} { {\mathbf{W}_R^k}^\top } {\mathbf{r}{i-j}^\top} }_\text{global positional bias}
$$
其中：

  • $\mathbf{p}j$ 被替换为相对位置编码 $\mathbf{r}{i-j} \in \mathbf{R}^{d}$;
  • $\mathbf{p}_i\mathbf{W}^q$ 被替换为两个可训练的参数 ${u}$ 和 ${v}$ ，分别用于计算content和location信息
  • $\mathbf{W}^k$ 被分成两个矩阵， $\mathbf{W}^k_E$ 处理content信息， $\mathbf{W}^k_R$ 处理location信息。

2. Reformer（ICLR 2020）

模型的关键思想：LSH(local sensitive hashing) attention ：附近的向量应获得相似的哈希值，而远距离的向量则不应获得相似的哈希值，因此被称为“局部敏感”。

Reformer(Kitaev, et al. 2020)主要解决了Transformer以下的几个问题：

  • 具有$N$层的模型中的内存是单层模型中的$N$倍。
  • 中间Feed Forward层通常相当大。
  • 长度为$L$的序列上的attention matrix 通常需要$O（L^2）$的内存和时间。

Reformer主要的改进为：

  • 将dot-product attention替换为 locality-sensitive hashing (LSH) attention，将复杂度从 $O(L^2)$ 降低到$O(L\log L)$。
  • 将残差模块替换为reversible的残差层，在训练期间仅存储一次激活（activation），而不是$N$次。
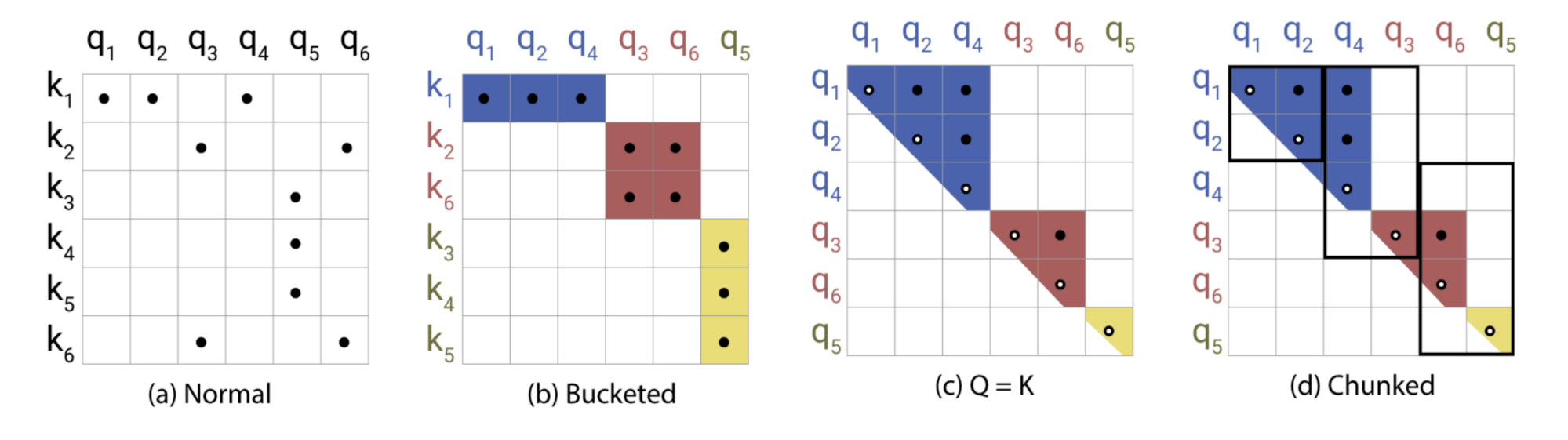
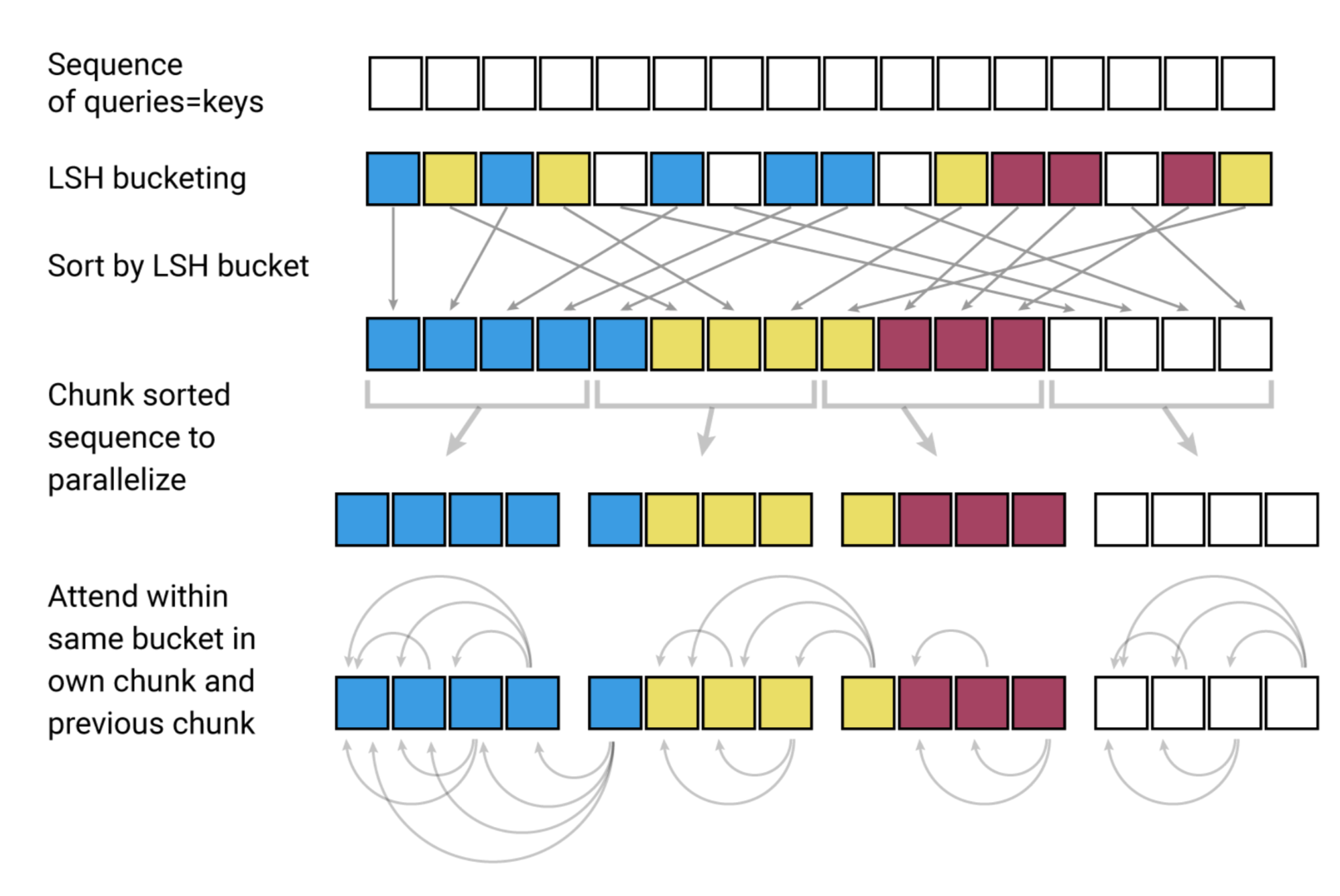
图9. LSH attention原理 (图片来源：Kitaev, et al. 2020）
图10. LSH attention的计算步骤 (图片来源：Kitaev, et al. 2020）

LSH attention

局部敏感哈希是一组将高维向量映射到一组离散值(桶/集群)的方法。它最常用来作为近似最近邻搜索的一种方法，用于近似的重复检测或视觉搜索等应用。

当哈希策略$x\rightarrow h(x)$ 是locality-sensitive的，那么就意味着它保留了数据点之间的距离信息，使得距离接近向量得到相似的哈希值，而距离较远向量有非常不同的哈希值。Reformer的哈希策略是：给定一个fixed random matrix $R \in R^{d \times b/2}$ ，哈希函数是：
$$
h(x)=argmax([xR;−xR])
$$
$[;]$表示concatenation。

为每个token计算一个桶之后，将根据它们的桶对这些token进行排序，并将标准的点积注意力应用到桶中的token的块上。有了足够多的桶，就减少了所有的给定的token需要处理的token的数量（论文的块取128）。

Reversible Residual Network

Reformer中使用了reversible residual layers (Gomez et al. 2017)。任何给定层的激活都可以从下一层的激活中恢复，只需使用模型参数。因此，我们可以通过在back propagation期间重新计算激活来节省内存，不需要存储所有激活。

reversible layer把输入和输出分成pairs： $(x1,x2)\rightarrow (y1,y2)$
$$
y1=x1+F(x2),y2=x2+G(y1)
$$
reverse：
$$
x2=y2−G(y1),x1=y1−F(x2)
$$
Sparse Transformer将reversible残差网络应用到传统的Transformer：
$$
Y1=X1+Attention(X2),\ Y2=X2+FeedForward(Y1)\Y1=X1+Attention(X2),\Y2=X2+FeedForward(Y1)
$$
在feed-forward计算中还可以被分块（chunking）：

$$
Y_2=[Y^{(1)}_2;…;Y^{(c)}_2]=[X^{(1)}_2+FeedForward(Y^{(1)}_1);…;X^{(c)}_2+FeedForward(Y^{(c)}_1)]
$$
reversible Transformer不需要存储每一层的activation。

3. Sparse Transformer

(Child et al., 2019) 通过稀疏矩阵分解，提出了factorized self-attention，使得在16384的序列长度上训练数百层的密集注意力网络成为可能，否则在硬件上是不可行的。

给定一组注意力连接模式（attention connectivity pattern） $\mathcal{S} = {S_1, \dots, S_n}$, 其中每个 $S_i$ 记录了第i个query vector的注意到的一组key position，有：

$$\begin{aligned} \text{Attend}(\mathbf{X}, \mathcal{S}) &= \Big( a(\mathbf{x}i, S_i) \Big){i \in {1, \dots, L}} \text{ where } a(\mathbf{x}i, S_i) = \text{softmax}\Big(\frac{(\mathbf{x}_i \mathbf{W}^q)(\mathbf{x}_j \mathbf{W}^k){j \in S_i}^\top}{\sqrt{d_k}}\Big) (\mathbf{x}j \mathbf{W}^v){j \in S_i} \end{aligned}$$

在自回归模型中，一个注意力范围（attention span）被定义为 $S_i = {j: j \leq i}$ ，它允许每个token关注过去的所有位置。

在factorized self-attention中, $S_i$ 会被分解成一个依赖关系的树，对每一对 $(i, j)$ 其中$j \leq i$, 都有一条将$i$ 连接到 $j$ 的路径 ，$j$ 可以直接或间接地注意到 $i$。

$S_i$被分成p个非重叠的子集，第m个子集表示为$A^{(m)}_i \subset S_i, m = 1,\dots, p$，输出位置$i$和任意一个$j$的最大距离为$p+1$。

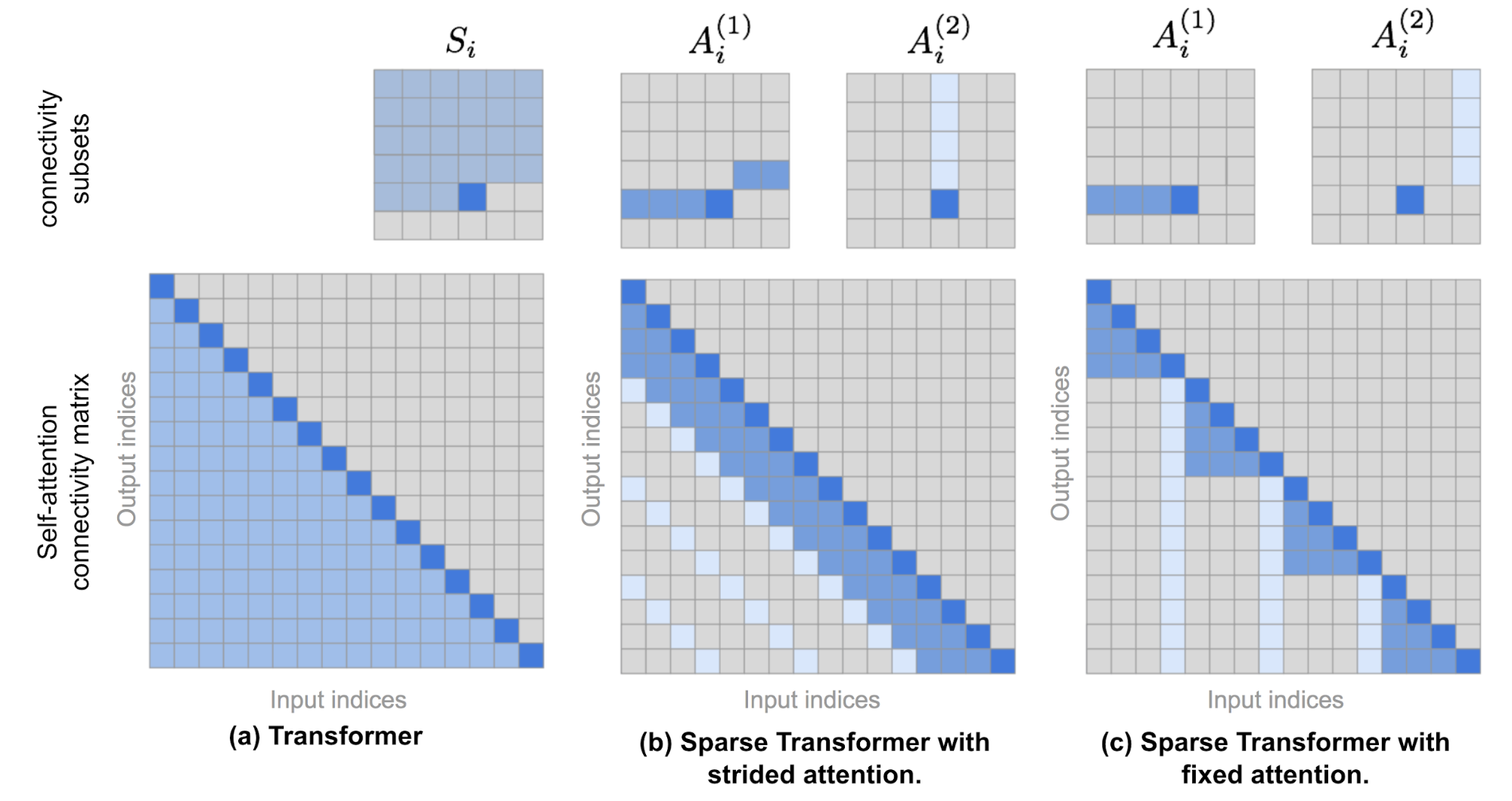
图11. Sparse Transformer的两种attention对比 （图片来源：Child, et al. 2020）

(1) Strided attention： 步幅为 $l - \sqrt{n}$ 。
$$
A^{(1)}_i={t,t+1,…,i}, where \space t=max(0,i−ℓ)\A^{(2)}={j:(i−j)\space mod\space ℓ=0}
$$
(2) Fixed attention：一个小的token的集合。
$$
A^{(1)}_i={j:⌊\frac{j}{ℓ}⌋=⌊\frac{i}{ℓ}⌋}\A^{(2)}_i={j:j\space mod\space ℓ∈{ℓ−c,…,ℓ−1}}
$$
c是超参数，文章选取 c∈{8,16,32} ，ℓ∈{128,256}。

4. Compressive Transformer（ICLR 2020）

“分而治之”的架构级别的改进，相当于在Transformer基础上添加了一个wrapper来增大有效上下文的长度

Compressive Transformer(Rae, et al. 2019)基于transformer-XL 方法进行改进，通过压缩memory 使得模型可以处理更长的序列，可长达一本书

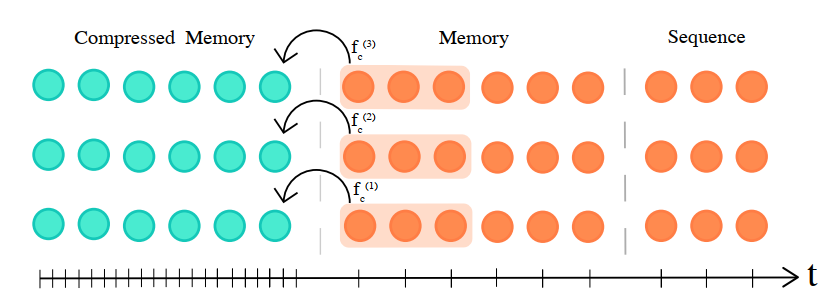
图12. Compressive Transformer原理图 （图片来源：Rae, et al. 2019）

将过去的隐藏activations映射到压缩后的表示（compressed memory）。

从短期的细粒度记忆和长期的粗粒度记忆学习query。旧的记忆不会被丢弃，而是被存储到了compressed memory中。

transformer-XL 会丢掉记忆窗口以外的信息，Compressive transformer 不会丢掉，而是把他们压缩并且存储到一个额外的记忆模块中，压缩函数如下：
$$
R^{n_s \times d} \rightarrow R^{\lfloor \frac{n_s}{c} \rfloor \times d}
$$
其中$d$是隐藏层的维度，$c$是压缩比例，$c$越大，压缩越多。

定义有2个memory： 一个是存放正常的前几个segment的隐藏状态，记为 $m$, 一个是存放压缩的记忆模块，记为$cm$。

假设原始序列为$S=(x_1 , x_2 , . . . x {|s|})$，将$S$切割成长度为$n_s$的大小的片段（segment），那么在$t$时刻模型输入的片段为：$X = x_t , …,x{t + n_s}$在$t$时刻得到的隐藏状态会放到放到先入先出队列$memory(m)$中，最早的将会被去除，然后通过一个压缩函数将被去除的隐藏状态压缩成更小的单元存放到$c_m$中。

在第$i$层中，$t$时刻时，模型先将$c_m$和$m$进行拼接得到第$i$层的记忆模块$mem$, 然后通过当前segment的隐藏状态和$mem$来计算多头注意力$a$, 后面进行layer norm，然后再处理记忆模块。将$m$中前$n_s$个记忆单元 放到$old_mem$中，并通过压缩函数生成新的$new_{cm}$。最后更新当前的memory和压缩记忆单元。

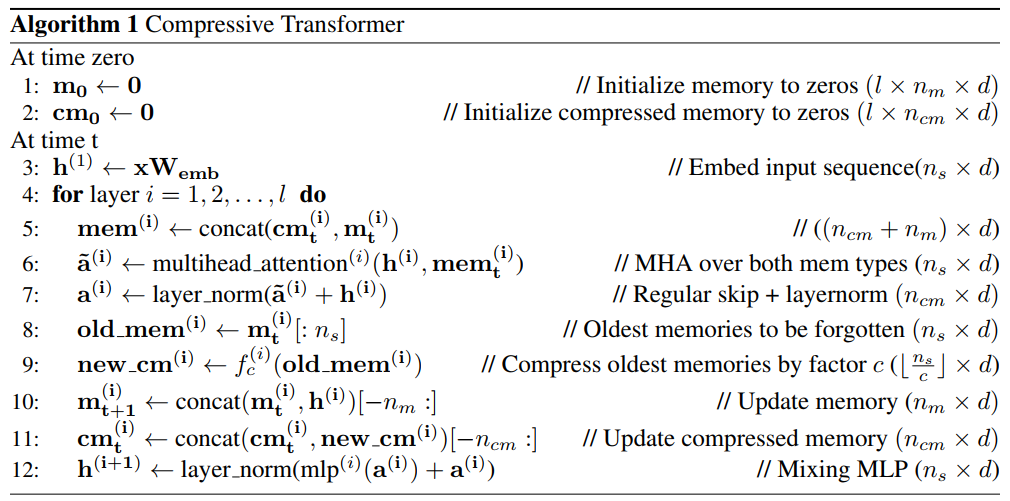
压缩函数 $f_c$可以选取：

  • max/mean pooling： kernel和步长设置为压缩比例 c。 这个是最快最简单的baseline。
  • 1D convolution ：kernel和步长也是设置为c。
  • dilated convolutions ：膨胀卷积。卷积压缩方法包含需要训练的参数。
  • most-used ：memories 存储 通过他们的平均attention 和最常使用来存储。这个来源于垃圾回收机制，不常用的记忆模块被删除掉。

压缩网络训练时，每个old memory 需要BPTT(backpropagating-through-time)，所以在训练时也考虑局部辅助压缩损失。

auto-encoding 损失 ：从压缩记忆模块中重建原始记忆，然后计算自编码的损失：
$$
L^{ae}=||old_mem^{(i)}-g(new_cm^{(i)})||_2
$$
其中$g: R^{\frac{n_s}{c} * d} \rightarrow R^{n_s * d}$。

上述是无损的压缩目标函数，试图从所有的记忆模块中恢复信息。
attention-reconstruction 损失：注意力重建损失。重建memory的上下文注意力损失，这个是有损失的目标函数，未被关注的信息已经丢失了。（这种损失表现更好。），计算伪代码如下：

5. Universal Transformer (ICLR 2019)

Transformer不是图灵完备的，有些很简单的任务表现很差，比如字符串拷贝。序列任务比较偏好于迭代和递归变换，RNN满足归纳偏置（Inductive Bias），但Transformer并不满足。

(Dehghani et al., 2019) 提出了universal Transformer，其中universal指的是computationally universal，即图灵完备。Universal Transformer主要的改进是加入对模型层数（depth）的循环。应用了一个机制对循环的次数进行控制。

和Transformer主要的区别：

  • 在Transformer中，输入在经过多头注意力层后会进入全连接层，而Universal Transformer会进入Transition层，通过共享权重的transition function继续循环计算。

  • positional embedding考虑time维度，每次循环会重新做一次coordinate embedding。

  • Weight sharing：归纳偏置是关于目标函数的假设，CNN和RNN分别假设空间平移不变性（spatial translation invariance）和时间平移不变性（time translation invariance），体现为CNN卷积核在空间上的权重共享和RNN单元在时间上的权重共享，所以universal transformer也增加了这种假设，使recurrent机制中的权重共享，在增加了模型表达力的同时更加接近RNN的归纳偏置。

  • Conditional computation：通过加入ACT控制模型的计算次数，比固定depth的Transformer，universal transformer取得了更好的结果。

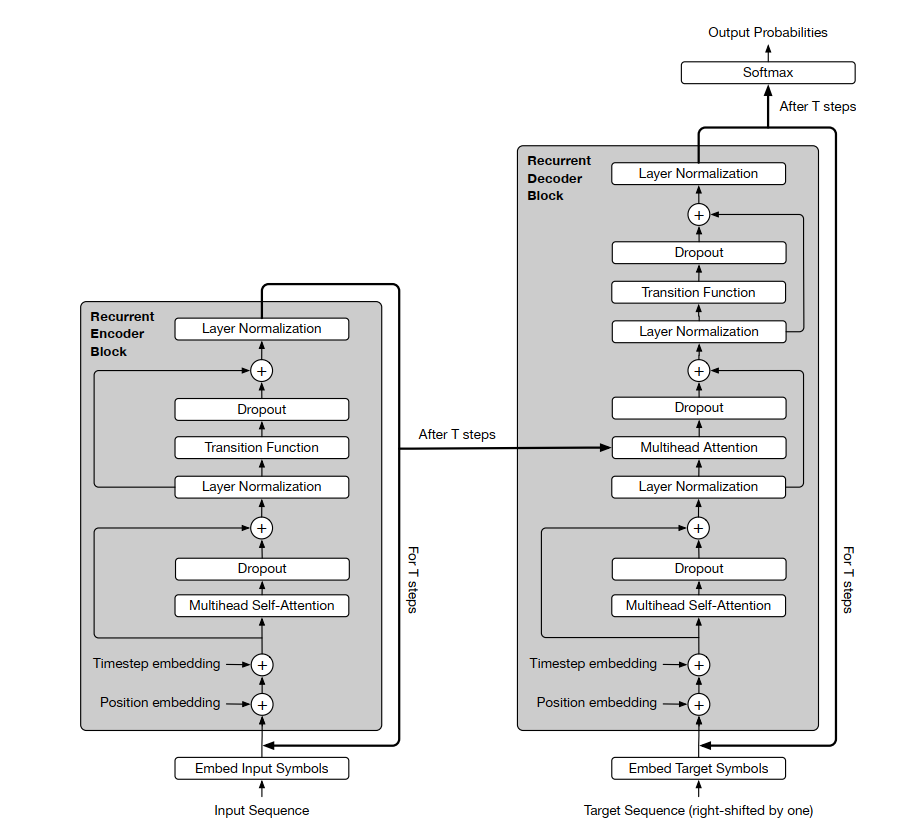
图13.Universal Attention原理图 （图片来源：Dehghani et al., 2019）

Transition Function

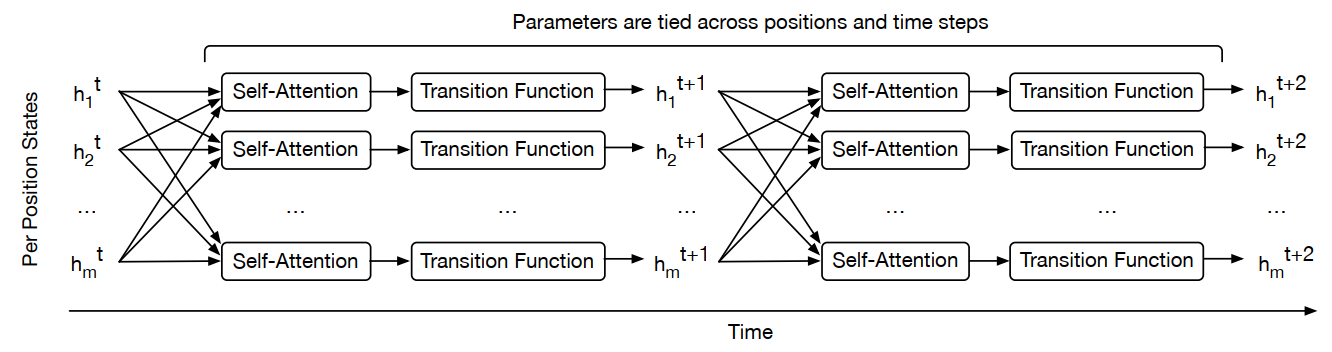
图14.Transition原理图 （图片来源：Dehghani et al., 2019）

Transition Function的两种选择：

1. separable convolution

2. fully-connected NN “consists of a single rectified-linear activation function between two affine transformations, applied position-wise” 。

这样，每个self-attention+transition的输出$H^t$可以表示为：
$$
H^t=LayerNorm(A^t+Transition(A^t)) \space where \space A^t=LayerNorm(H^{t-1}+P^t)
$$

Coordinate embeddings

Transformer的positional embedding只用考虑symbol的position就可以了，这里又多了一个time维度，所以每一次循环都会重新做一次coordinate embedding。Embedding公式如下：
$$
P_{pos,2j}^t=sin(pos/10000^{2j/d} \oplus sin(t/10000^{2j/d}))\
P_{pos,2j+1}^t=cos(pos/10000^{2j/d} \oplus cos(t/10000^{2j/d}))
$$

Adaptive Computation Time (ACT)

  • ACT(Graves,2016)：a mechanism for dynamically modulating the number of computational steps needed to process each input symbol
  • 可以模型会动态调整每个位置所需的计算steps。每个position的ACT是独立的，如果一个position a在t时刻被停止了， $h_a^t$会被一直复制到最后一个position停止，当然也会设置一个最大时间，避免死循环。 当所有位置都停止计算后，整个过程才停止。

6. Linear Transformer （ICLR 2020）/ Performer（ICLR 2021）

从结构上对 Attention 进行修改从而降低其计算复杂度，Linear Transformer(Katharopoulos et al.,2020)主要思想是：去掉标准 Attention 中的 Softmax，使得 Attention 的复杂度退化为O（n）级别（Linear Attention）。

在Transformer中广泛使用的scaled dot-product注意力机制中，$Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt{d_k}})V=AV$，在计算时，softmax内部的$QK^T$会先进行计算，需要$O(MN) $的空间储存注意力矩阵，因此在$M $和 $N $很大时（例如对一个长序列算自注意力)，会存在计算瓶颈问题，造成内存爆炸。

一种改进的思路是使用核函数替代softmax+内积的相似度计算。实际上，更广义的注意力计算是使用一个相似性度量选择记忆中要获取（retrieve）的值向量:

$$
h_i=\Sigma_j\frac{sim(q_i,k_j)}{\Sigma_l sim(q_i,k_l)}v_j
$$
在scaled dot-product attention中，我们令 $sim(x,y)=exp(\gamma x^Ty)$，而线性注意力将$sim(x,y)$ 用两个核函数的内积替代

$$
sim(x,y)=\phi(x)^T\phi(y)
$$
相当于将核函数反过来用。通过解耦相似度度量，可获得：
$$
h_i=\Sigma_j\frac{\phi(q_i)^T\phi(k_j)}{\Sigma_l sim(\phi(q_i)^T\phi(k_l))}v_j \
=\frac{\phi(q_i)^T\textcolor{blue}{\Sigma_j\phi(k_j)\otimes v_j}}{\Sigma_l sim(\phi(q_i)^T\textcolor{blue}{\Sigma_j\phi(k_j))}}
$$
注意到(5)式中的求和（蓝色部分）均可以先一遍计算，复杂度$O(M)$ ，然后计算与$\phi(q_i)$ 逐一计算内积并归一化(复杂度为$O(N)$，不再需要存储复杂度为$O(MN)$的中间矩阵。Linear Trasformer和传统Transformer的区别如下图：

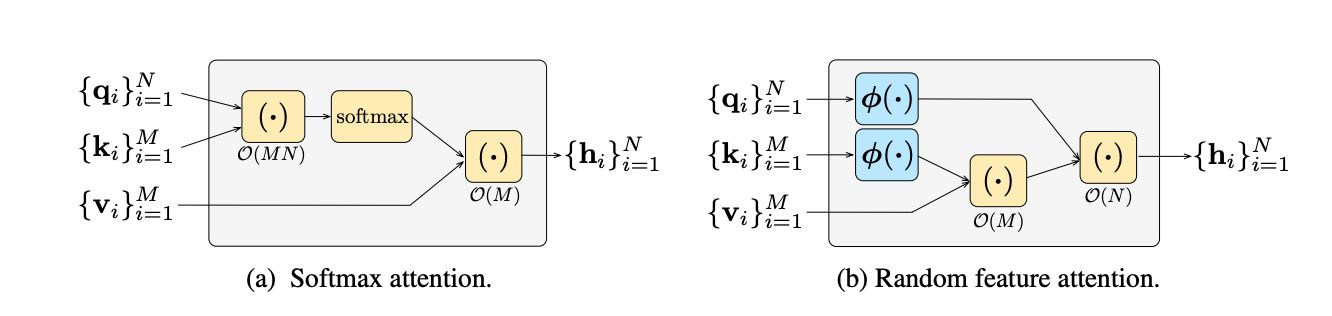
图15. 传统注意力与线性注意力的区别 （图片来源：Random Feature Attention）

2020年采用这一思路的代表工作两个，一个是Linear Transformer，另一个是Performer。

它们的主要差别在于使用了不同的特征映射$\phi(\cdot)$。其中Linear Transformer使用了简单的特征映射$\phi(x)_i=elu(x_i)$，而Performer(Choromanski et al.,2021)则从无偏逼近softmax函数的角度出发，使用了随机特征映射，其中第一版Performer是根据高斯核的傅立叶分解（借用了SVM时期的思想），第二版Performer则将这种随机特征映射替换为了正定的特征映射（使得softmax的逼近更稳定)。

7. Linformer

Linformer(Wang et al.,2020)中用了较大的篇幅证注意力矩阵是低秩矩阵（通过以下的两个Theorem），所以用低秩近似取代原有的全注意力机制。

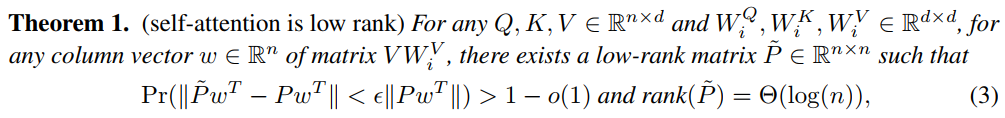
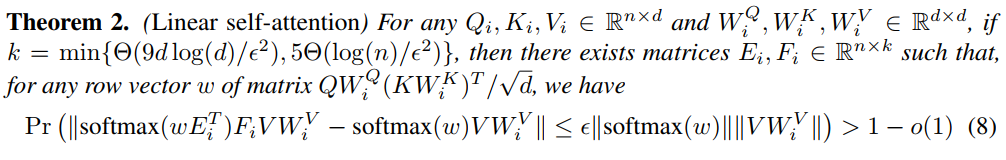
从某种程度上来说，将$n\times d$的输入映射到$k\times d$的维度其实是对输入序列做了卷积池化，把原来每个token的信息进行二次融合，去除冗余部分，得到更精炼的向量表示。简而言之，同样的信息，用更少更丰富的语义向量去表达。

总结

Transformer被提出后，产生了很多变种的Transformer，大部分的模型是从Transformer本身的模型设计和架构出发，对模型进行改进，主要集中解决了Transformer计算复杂度高、难以处理长文本、图灵不完备等问题。在降低计算复杂度的问题上，主要就包括限制attention的范围、利用memory、使用低秩的矩阵等方法。

参考文献

[1] A Survey of Transformers

[2] Efficient Transformer A survey

[3] Kitaev, Nikita, Łukasz Kaiser, and Anselm Levskaya. “Reformer: The efficient transformer.” ICLR, 2020.

[4] Zihang Dai, et al. “Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context.” ACL 2019.

[5] Aidan N. Gomez, et al. “The Reversible Residual Network: Backpropagation Without Storing Activations” NIPS 2017.

[6] Child, Rewon, et al. “Generating long sequences with sparse transformers.” arXiv preprint arXiv:1904.10509 (2019).

[7] Dehghani, M. , et al. “Universal Transformers.” ICLR, 2019.

[8] ack W. Rae, et al. “Compressive transformers for long-range sequence modelling.” ICLR, 2020.

[9] Angelos Katharopoulos, et al. “Transformers are rnns: Fast autoregressive transformers with linear attention.” ICLR, 2020.

[10] Krzysztof Choromanski, et al. “Attention with Performers” ICLR, 2021.

[11] Sinong Wang, et al.“Linformer: Selfattention with linear complexity”. arXiv preprint arXiv:2006.04768, 2020b.